EPR paradox
| Quantum mechanics | ||||||||||||||||
 |
||||||||||||||||
| Uncertainty principle |
||||||||||||||||
Introduction · Mathematical formulations
|
||||||||||||||||
The EPR paradox (or Einstein–Podolsky–Rosen paradox) refers to a dichotomy, where either the measurement of a physical quantity in one system affects the measurement of a physical quantity in another, spatially separated system or the description of reality given by a wave function is not complete. This challenge to the Copenhagen interpretation originated from the consequences of a thought experiment introduced in 1935 by Einstein, Podolsky, and Rosen and resulted in what seemed to be a contradiction in the interpretation.[1]
Einstein never accepted quantum mechanics as a "real" and complete theory, struggling to the end of his life for a theory that could better comply with causality, and protesting against the view that there exists no objective physical reality other than that which is revealed through measurement as it is interpreted in terms of the quantum mechanical formalism.
The EPR paradox is a paradox in the following sense: if one adds to quantum mechanics some seemingly reasonable but apparently otherwise hidden variables that supposedly express the concept of local realism (not to be confused with philosophical realism; see Bell inequality, Bell test experiments, and counterfactual definiteness) — then one obtains a contradiction. However, quantum mechanics by itself, without the Copenhagen interpretation, does not appear to be internally inconsistent, nor — as it turns out — does it contradict causality, though enthusiasts of the Bell persuasion assert that it does so, on the basis of the EPR paradox. Some physicists today regard the EPR paradox as an illustration of how quantum mechanics violates classical intuitions.
Contents |
Quantum mechanics and its interpretation
Since the early twentieth century, quantum theory has proved to be very successful, describing accurately the physical reality of the mesoscopic and microscopic world. This fact has been made clear through multiple and repeatable physical experiments.
Quantum mechanics was developed with the aim of describing atoms and explaining the observed spectral lines in a measurement apparatus. Though disputed, it has never been seriously challenged. Philosophical interpretations of quantum phenomena, however, are another story: the question of how to interpret the mathematical formulation of quantum mechanics has given rise to a variety of different answers from people of different philosophical backgrounds (see Interpretation of quantum mechanics).
Quantum theory and quantum mechanics do not account for single measurement outcomes in a deterministic way. According to an accepted interpretation of quantum mechanics known as the Copenhagen interpretation, a measurement causes an instantaneous collapse of the wave function describing the quantum system into an eigenstate of the observable that was measured.
The most prominent opponent of the Copenhagen interpretation was Albert Einstein. In his view, quantum mechanics is incomplete and, commenting on this, other writers (such as John von Neumann[2] and David Bohm[3]) though not Einstein himself, have suggested that consequently there would have to be 'hidden' variables responsible for random measurement results.
The famous paper "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?"[1], authored by Einstein, Podolsky and Rosen in 1935, condensed the philosophical discussion into a physical argument. They claim that given a specific experiment, in which the outcome of a measurement could be known before the measurement takes place, there must exist something in the real world, an "element of reality", which determines the measurement outcome. They postulate that these elements of reality are local, in the sense that each belongs to a certain point in spacetime. Each element may only be influenced by events which are located in the backward light cone of its point in spacetime. These claims are founded on assumptions about nature which constitute what is now known as local realism.
Though the EPR paper has often been taken as an exact expression of Einstein's views, it was primarily authored by Podolsky, based on discussions at the Institute for Advanced Study with Einstein and Rosen. Einstein later expressed to Erwin Schrödinger that "It did not come out as well as I had originally wanted; rather, the essential thing was, so to speak, smothered by the formalism."[4] In 1948 Einstein presented a less formal account of his local realist ideas.
Description of the paradox
The EPR paradox draws on a phenomenon predicted by quantum mechanics, known as quantum entanglement, to show that measurements performed on spatially separated parts of a quantum system can apparently have an instantaneous influence on one another.
This effect is now known as "nonlocal behavior" (or colloquially as "quantum weirdness" or "spooky action at a distance").
Simple version
Before delving into the complicated logic that leads to the 'paradox', it is perhaps worth mentioning the simple version of the argument, as described by Greene and others, which Einstein used to show that 'hidden variables' must exist.
A positron and an electron are emitted from a source, by pion decay, so that their spins are opposite; one particle’s spin about any axis is the negative of the other's. Also, due to uncertainty, making a measurement of a particle’s spin about one axis disturbs the particle so you now can’t measure its spin about any other axis.
Now say you measure the electron’s spin about the x-axis. This automatically tells you the positron’s spin about the x-axis. Since you’ve done the measurement without disturbing the positron in any way, it can’t be that the positron "only came to have that state when you measured it", because you didn’t measure it! It must have had that spin all along. Also you can now measure the positron’s spin about the y-axis. So it follows that the positron has had a definite spin about two axes – much more information than the positron is capable of holding, and a "hidden variable" according to some interpretations of EPR.
Measurements on an entangled state
We have a source that emits electron-positron pairs, with the electron sent to destination A, where there is an observer named Alice, and the positron sent to destination B, where there is an observer named Bob. According to quantum mechanics, we can arrange our source so that each emitted pair occupies a quantum state called a spin singlet. This can be viewed as a quantum superposition of two states, which we call state I and state II. In state I, the electron has spin pointing upward along the z-axis (+z) and the positron has spin pointing downward along the z-axis (-z). In state II, the electron has spin -z and the positron has spin +z. Therefore, it is impossible to associate either particle in the spin singlet with a state of definite spin. The particles are thus said to be entangled.
Alice now measures the spin along the z-axis. She can obtain one of two possible outcomes: +z or -z. Suppose she gets +z. According to quantum mechanics, the quantum state of the system collapses into state I. (Different interpretations of quantum mechanics have different ways of saying this, but the basic result is the same.) The quantum state determines the probable outcomes of any measurement performed on the system. In this case, if Bob subsequently measures spin along the z-axis, he will obtain -z with 100% probability. Similarly, if Alice gets -z, Bob will get +z.
There is, of course, nothing special about our choice of the z-axis. For instance, suppose that Alice and Bob now decide to measure spin along the x-axis, according to quantum mechanics, the spin singlet state may equally well be expressed as a superposition of spin states pointing in the x direction. We'll call these states Ia and IIa. In state Ia, Alice's electron has spin +x and Bob's positron has spin -x. In state IIa, Alice's electron has spin -x and Bob's positron has spin +x. Therefore, if Alice measures +x, the system collapses into Ia, and Bob will get -x. If Alice measures -x, the system collapses into IIa, and Bob will get +x.
In quantum mechanics, the x-spin and z-spin are "incompatible observables", which means that there is a Heisenberg uncertainty principle operating between them: a quantum state cannot possess a definite value for both variables. Suppose Alice measures the z-spin and obtains +z, so that the quantum state collapses into state I. Now, instead of measuring the z-spin as well, Bob measures the x-spin. According to quantum mechanics, when the system is in state I, Bob's x-spin measurement will have a 50% probability of producing +x and a 50% probability of -x. Furthermore, it is fundamentally impossible to predict which outcome will appear until Bob actually performs the measurement.
Here is the crux of the matter. You might imagine that, when Bob measures the x-spin of his positron, he would get an answer with absolute certainty, since prior to this he hasn't disturbed his particle at all. But, as described above, Bob's positron has a 50% probability of producing +x and a 50% probability of -x—random behaviour, not certain. Bob's positron knows that Alice's electron has been measured, and its z-spin detected, and hence B's z-spin calculated, so its x-spin is 'out of bounds'.
Put another way, how does Bob's positron know, at the same time, which way to point if Alice decides (based on information unavailable to Bob) to measure x (i.e. be the opposite of Alice's electron's spin about the x-axis) and also how to point if Alice measures z (i.e. behave randomly), since it is only supposed to know one thing at a time? Using the usual Copenhagen interpretation rules that say the wave function "collapses" at the time of measurement, there must be action at a distance (entanglement) or the positron must know more than it is supposed to (hidden variables).
In case the explanation above is confusing, here is the paradox summed up:
An electron-positron pair is emitted, the particles shoot off and are measured later. Whatever axis their spins are measured along, they are always found to be opposite. This can only be explained if the particles are linked in some way. Either they were created with a definite (opposite) spin about every axis—a "hidden variable" argument—or they are linked so that one electron knows what axis the other is having its spin measured along, and becomes its opposite about that one axis—an "entanglement" argument. Moreover, if the two particles have their spins measured about different axes, once the electron's spin has been measured about the x-axis (and the positron's spin about the x-axis deduced), the positron's spin about the y-axis will no longer be certain, as if it knows that the measurement has taken place. Either that or it has a definite spin already, which gives it a spin about a second axis—a hidden variable.
Incidentally, although we have used spin as an example, many types of physical quantities—what quantum mechanics refers to as "observables"—can be used to produce quantum entanglement. The original EPR paper used momentum for the observable. Experimental realizations of the EPR scenario often use photon polarization, because polarized photons are easy to prepare and measure.
Locality in the EPR experiment
The principle of locality states that physical processes occurring at one place should have no immediate effect on the elements of reality at another location. At first sight, this appears to be a reasonable assumption to make, as it seems to be a consequence of special relativity, which states that information can never be transmitted faster than the speed of light without violating causality. It is generally believed that any theory which violates causality would also be internally inconsistent, and thus deeply unsatisfactory.
It turns out that the usual rules for combining quantum mechanical and classical descriptions violate the principle of locality without violating causality. Causality is preserved because there is no way for Alice to transmit messages (i.e. information) to Bob by manipulating her measurement axis. Whichever axis she uses, she has a 50% probability of obtaining "+" and 50% probability of obtaining "-", completely at random; according to quantum mechanics, it is fundamentally impossible for her to influence what result she gets. Furthermore, Bob is only able to perform his measurement once: there is a fundamental property of quantum mechanics, known as the "no cloning theorem", which makes it impossible for him to make a million copies of the electron he receives, perform a spin measurement on each, and look at the statistical distribution of the results. Therefore, in the one measurement he is allowed to make, there is a 50% probability of getting "+" and 50% of getting "-", regardless of whether or not his axis is aligned with Alice's.
However, the principle of locality appeals powerfully to physical intuition, and Einstein, Podolsky and Rosen were unwilling to abandon it. Einstein derided the quantum mechanical predictions as "spooky action at a distance". The conclusion they drew was that quantum mechanics is not a complete theory.
In recent years, however, doubt has been cast on EPR's conclusion due to developments in understanding locality and especially quantum decoherence. The word locality has several different meanings in physics. For example, in quantum field theory "locality" means that quantum fields at different points of space do not interact with one another. However, quantum field theories that are "local" in this sense appear to violate the principle of locality as defined by EPR, but they nevertheless do not violate locality in a more general sense. Wavefunction collapse can be viewed as an epiphenomenon of quantum decoherence, which in turn is nothing more than an effect of the underlying local time evolution of the wavefunction of a system and all of its environment. Since the underlying behaviour doesn't violate local causality, it follows that neither does the additional effect of wavefunction collapse, whether real or apparent. Therefore, as outlined in the example above, neither the EPR experiment nor any quantum experiment demonstrates that faster-than-light signaling is possible.
Resolving the paradox
Hidden variables
There are several ways to resolve the EPR paradox. The one suggested by EPR is that quantum mechanics, despite its success in a wide variety of experimental scenarios, is actually an incomplete theory. In other words, there is some yet undiscovered theory of nature to which quantum mechanics acts as a kind of statistical approximation (albeit an exceedingly successful one). Unlike quantum mechanics, the more complete theory contains variables corresponding to all the "elements of reality". There must be some unknown mechanism acting on these variables to give rise to the observed effects of "non-commuting quantum observables", i.e. the Heisenberg uncertainty principle. Such a theory is called a hidden variable theory.
To illustrate this idea, we can formulate a very simple hidden variable theory for the above thought experiment. One supposes that the quantum spin-singlet states emitted by the source are actually approximate descriptions for "true" physical states possessing definite values for the z-spin and x-spin. In these "true" states, the electron going to Bob always has spin values opposite to the electron going to Alice, but the values are otherwise completely random. For example, the first pair emitted by the source might be "(+z, -x) to Alice and (-z, +x) to Bob", the next pair "(-z, -x) to Alice and (+z, +x) to Bob", and so forth. Therefore, if Bob's measurement axis is aligned with Alice's, he will necessarily get the opposite of whatever Alice gets; otherwise, he will get "+" and "-" with equal probability.
Assuming we restrict our measurements to the z and x axes, such a hidden variable theory is experimentally indistinguishable from quantum mechanics. In reality, of course, there is an (uncountably) infinite number of axes along which Alice and Bob can perform their measurements, so there has to be an infinite number of independent hidden variables. However, this is not a serious problem; we have formulated a very simplistic hidden variable theory, and a more sophisticated theory might be able to patch it up. It turns out that there is a much more serious challenge to the idea of hidden variables.
Bell's inequality
In 1964, John Bell showed that the predictions of quantum mechanics in the EPR thought experiment are significantly different from the predictions of a very broad class of hidden variable theories (the local hidden variable theories). Roughly speaking, quantum mechanics predicts much stronger statistical correlations between the measurement results performed on different axes than the hidden variable theories. These differences, expressed using inequality relations known as "Bell's inequalities", are in principle experimentally detectable. Later work by Eberhard showed that the key properties of local hidden variable theories that lead to Bell's inequalities are locality and counter-factual definiteness. Any theory in which these principles hold produces the inequalities. A. Fine subsequently showed that any theory satisfying the inequalities can be modeled by a local hidden variable theory.
After the publication of Bell's paper, a variety of experiments were devised to test Bell's inequalities. (As mentioned above, these experiments generally rely on photon polarization measurements.) All the experiments conducted to date have found behavior in line with the predictions of standard quantum mechanics.
However, Bell's theorem does not apply to all possible philosophically realist theories, although a common misconception is that quantum mechanics is inconsistent with all notions of philosophical realism. Realist interpretations of quantum mechanics are possible, although as discussed above, such interpretations must reject either locality or counter-factual definiteness. Mainstream physics prefers to keep locality while still maintaining a notion of realism that nevertheless rejects counter-factual definiteness. Examples of such mainstream realist interpretations are the consistent histories interpretation and the transactional interpretation. Fine's work showed that taking locality as a given there exist scenarios in which two statistical variables are correlated in a manner inconsistent with counter-factual definiteness and that such scenarios are no more mysterious than any other despite the inconsistency with counter-factual definiteness seeming 'counter-intuitive'. Violation of locality however is difficult to reconcile with special relativity and is thought to be incompatible with the principle of causality. On the other hand the Bohm interpretation of quantum mechanics instead keeps counter-factual definiteness while introducing a conjectured non-local mechanism called the 'quantum potential'. Some workers in the field have also attempted to formulate hidden variable theories that exploit loopholes in actual experiments, such as the assumptions made in interpreting experimental data although no such theory has been produced that can reproduce all the results of quantum mechanics.
There are also individual EPR-like experiments that have no local hidden variables explanation. Examples have been suggested by David Bohm and by Lucien Hardy.
Einstein's hope for a purely algebraic theory
The Bohm interpretation of quantum mechanics hypothesizes that the state of the universe evolves smoothly through time with no collapsing of quantum wavefunctions. One problem for the Copenhagen interpretation is to precisely define wavefunction collapse. Einstein maintained that quantum mechanics is physically incomplete and logically unsatisfactory. In "The Meaning of Relativity," Einstein wrote, "One can give good reasons why reality cannot at all be represented by a continuous field. From the quantum phenomena it appears to follow with certainty that a finite system of finite energy can be completely described by a finite set of numbers (quantum numbers). This does not seem to be in accordance with a continuum theory and must lead to an attempt to find a purely algebraic theory for the representation of reality. But nobody knows how to find the basis for such a theory." If time, space, and energy are secondary features derived from a substrate below the Planck scale, then Einstein's hypothetical algebraic system might resolve the EPR paradox (although Bell's theorem would still be valid). Edward Fredkin in the Fredkin Finite Nature Hypothesis has suggested an informational basis for Einstein's hypothetical algebraic system. If physical reality is totally finite, then the Copenhagen interpretation might be an approximation to an information processing system below the Planck scale.
"Acceptable theories", and the experiment
According to the present view of the situation, quantum mechanics simply contradicts Einstein's philosophical postulate that any acceptable physical theory should fulfill "local realism".
In the EPR paper (1935) the authors realized that quantum mechanics was non-acceptable in the sense of their above-mentioned assumptions, and Einstein thought erroneously that it could simply be augmented by 'hidden variables', without any further change, to get an acceptable theory. He pursued these ideas until the end of his life (1955), over twenty years.
In contrast, John Bell, in his 1964 paper, showed "once and for all" that quantum mechanics and Einstein's assumptions lead to different results, different by a factor of 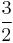 , for certain correlations. So the issue of "acceptability", up to this time mainly concerning theory (even philosophy), finally became experimentally decidable.
, for certain correlations. So the issue of "acceptability", up to this time mainly concerning theory (even philosophy), finally became experimentally decidable.
There are many Bell test experiments hitherto, e.g. those of Alain Aspect and others. They all show that pure quantum mechanics, and not Einstein's "local realism", is acceptable. Thus, according to Karl Popper these experiments falsify Einstein's philosophical assumptions, especially the ideas on "hidden variables", whereas quantum mechanics itself remains a good candidate for a theory, which is acceptable in a wider context.
Implications for quantum mechanics
Most physicists today believe that quantum mechanics is correct, and that the EPR paradox is a "paradox" only because classical intuitions do not correspond to physical reality. How EPR is interpreted regarding locality depends on the interpretation of quantum mechanics one uses. In the Copenhagen interpretation, it is usually understood that instantaneous wavefunction collapse does occur. However, the view that there is no causal instantaneous effect has also been proposed within the Copenhagen interpretation: in this alternate view, measurement affects our ability to define (and measure) quantities in the physical system, not the system itself. In the many-worlds interpretation, a kind of locality is preserved, since the effects of irreversible operations such as measurement arise from the relativization of a global state to a subsystem such as that of an observer.
The EPR paradox has deepened our understanding of quantum mechanics by exposing the fundamentally non-classical characteristics of the measurement process. Prior to the publication of the EPR paper, a measurement was often visualized as a physical disturbance inflicted directly upon the measured system. For instance, when measuring the position of an electron, one imagines shining a light on it, thus disturbing the electron and producing the quantum mechanical uncertainties in its position. Such explanations, which are still encountered in popular expositions of quantum mechanics, are debunked by the EPR paradox, which shows that a "measurement" can be performed on a particle without disturbing it directly, by performing a measurement on a distant entangled particle.
Technologies relying on quantum entanglement are now being developed. In quantum cryptography, entangled particles are used to transmit signals that cannot be eavesdropped upon without leaving a trace. In quantum computation, entangled quantum states are used to perform computations in parallel, which may allow certain calculations to be performed much more quickly than they ever could be with classical computers.
Mathematical formulation
The above discussion can be expressed mathematically using the quantum mechanical formulation of spin. The spin degree of freedom for an electron is associated with a two-dimensional Hilbert space H, with each quantum state corresponding to a vector in that space. The operators corresponding to the spin along the x, y, and z direction, denoted Sx, Sy, and Sz respectively, can be represented using the Pauli matrices:
where  stands for Planck's constant divided by 2π.
stands for Planck's constant divided by 2π.
The eigenstates of Sz are represented as
and the eigenstates of Sx are represented as
The Hilbert space of the electron pair is  , the tensor product of the two electrons' Hilbert spaces. The spin singlet state is
, the tensor product of the two electrons' Hilbert spaces. The spin singlet state is
where the two terms on the right hand side are what we have referred to as state I and state II above.
From the above equations, it can be shown that the spin singlet can also be written as
where the terms on the right hand side are what we have referred to as state Ia and state IIa.
To illustrate how this leads to the violation of local realism, we need to show that after Alice's measurement of Sz (or Sx), Bob's value of Sz (or Sx) is uniquely determined, and therefore corresponds to an "element of physical reality". This follows from the principles of measurement in quantum mechanics. When Sz is measured, the system state ψ collapses into an eigenvector of Sz. If the measurement result is +z, this means that immediately after measurement the system state undergoes an orthogonal projection of ψ onto the space of states of the form
For the spin singlet, the new state is
Similarly, if Alice's measurement result is -z, the system undergoes an orthogonal projection onto
which means that the new state is
This implies that the measurement for Sz for Bob's electron is now determined. It will be -z in the first case or +z in the second case.
It remains only to show that Sx and Sz cannot simultaneously possess definite values in quantum mechanics. One may show in a straightforward manner that no possible vector can be an eigenvector of both matrices. More generally, one may use the fact that the operators do not commute,
along with the Heisenberg uncertainty relation
See also
|
|
References
Selected papers
- A. Aspect, Bell's inequality test: more ideal than ever, Nature 398 189 (1999). [2]
- J.S. Bell, On the Einstein-Poldolsky-Rosen paradox, Physics 1 195bbcv://prola.aps.org/abstract/PR/v48/i8/p696_1]
- P.H. Eberhard, Bell's theorem without hidden variables. Nuovo Cimento 38B1 75 (1977).
- P.H. Eberhard, Bell's theorem and the different concepts of locality. Nuovo Cimento 46B 392 (1978).
- A. Einstein, B. Podolsky, and N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47 777 (1935). [3]
- A. Fine, Hidden Variables, Joint Probability, and the Bell Inequalities. Phys. Rev. Lett. 48, 291 (1982).[4]
- A. Fine, Do Correlations need to be explained?, in Philosophical Consequences of Quantum Theory: Reflections on Bell's Theorem, edited by Cushing & McMullin (University of Notre Dame Press, 1986).
- L. Hardy, Nonlocality for two particles without inequalities for almost all entangled states. Phys. Rev. Lett. 71 1665 (1993).[5]
- M. Mizuki, A classical interpretation of Bell's inequality. Annales de la Fondation Louis de Broglie 26 683 (2001).
- P. Pluch, "Theory for Quantum Probability", PhD Thesis University of Klagenfurt (2006)
- M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe and D. J. Wineland, Experimental violation of a Bell's inequality with efficient detection, Nature 409, 791-794 (15 February 2001). [6]
- M. Smerlak, C. Rovelli, Relational EPR [7]
Notes
- ↑ Einstein, A; B Podolsky, N Rosen (1935-05-15). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?". Physical Review 47 (10): 777–80. doi: 10.1103/PhysRev.47.777. http://prola.aps.org/pdf/PR/v47/i10/p777_1. Retrieved 2010-08-19.
- ↑ von Neumann, J. (1932/1955). In Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, translated into English by Beyer, R.T., Princeton University Press, Princeton, cited by Baggott, J. (2004) Beyond Measure: Modern physics, philosophy, and the meaning of quantum theory, Oxford University Press, Oxford, ISBN 0198529279, pages 144-145.
- ↑ Bohm, D. (1951). Quantum Theory, Prentice-Hall, Englewood Cliffs, page 29, and Chapter 5 section 3, and Chapter 22 Section 19.
- ↑ Quoted in Kaiser, David. "Bringing the human actors back on stage: the personal context of the Einstein-Bohr debate," British Journal for the History of Science 27 (1994): 129-152, on page 147.
Books
- John S. Bell (1987) Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. ISBN 0-521-36869-3.
- Arthur Fine (1996) The Shaky Game: Einstein, Realism and the Quantum Theory, 2nd ed. Univ. of Chicago Press.
- J.J. Sakurai, J. J. (1994) Modern Quantum Mechanics. Addison-Wesley: 174–187, 223-232. ISBN 0-201-53929-2.
- Selleri, F. (1988) Quantum Mechanics Versus Local Realism: The Einstein-Podolsky-Rosen Paradox. New York: Plenum Press. ISBN 0-306-42739-7
- Leon Lederman, L., Teresi, D. (1993). The God Particle: If the Universe is the Answer, What is the Question? Houghton Mifflin Company, pages 21, 187 to 189.
External links
- The Einstein-Podolsky-Rosen Argument in Quantum Theory; 1.2 The argument in the text;
http://plato.stanford.edu/entries/qt-epr/#1.2 - The original EPR paper.
- Stanford Encyclopedia of Philosophy: "The Einstein-Podolsky-Rosen Argument in Quantum Theory" by Arthur Fine.
- Abner Shimony (2004) "Bell’s Theorem."
- EPR, Bell & Aspect: The Original References.
- Does Bell's Inequality Principle rule out local theories of quantum mechanics? From the Usenet Physics FAQ.
- Theoretical use of EPR in teleportation.
- Effective use of EPR in cryptography.
- EPR experiment with single photons interactive.
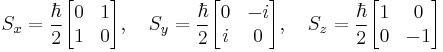
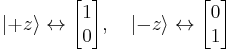

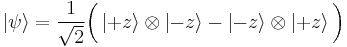
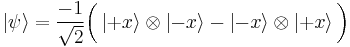
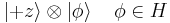
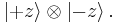

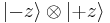
![\left[ S_x, S_z\right] = - i\hbar S_y \ne 0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c50635b06f39ce6a70626bfdeab43f21.png)
![\lang (\Delta S_x)^2 \rang \lang (\Delta S_z)^2 \rang \ge
\frac{1}{4} \left|\lang \left[ S_x, S_z\right] \rang \right|^2](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b614b8b7e63d3be901265718ff5aa9c0.png)